Эмпирические прогностические модели сложных систем
В ИПФ РАН разработан подход к описанию процессов, протекающих в сложных (высокоразмерных) системах, основанный на построении эмпирических низкоразмерных моделей в форме случайных динамических систем (А. М. Фейгин, Е. М. Лоскутов, Д. Н. Мухин). Возрастающий с каждым годом интерес к задачам прогностической реконструкции (построению параметризованных неавтономных математических моделей) систем, порождающих наблюдаемые процессы, связан со сложностью изучаемых в различных областях науки природных объектов, не позволяющей во многих случаях создавать обладающие необходимой универсальностью и грубостью модели на основании первых принципов. С другой стороны, разработанные к настоящему времени методы построения моделей оператора эволюции системы по временным рядам оказываются неприменимы к анализу реальных данных в силу высокой размерности исследуемой системы, существенной случайной компоненты, ограниченности исследуемой выборки и т. д.
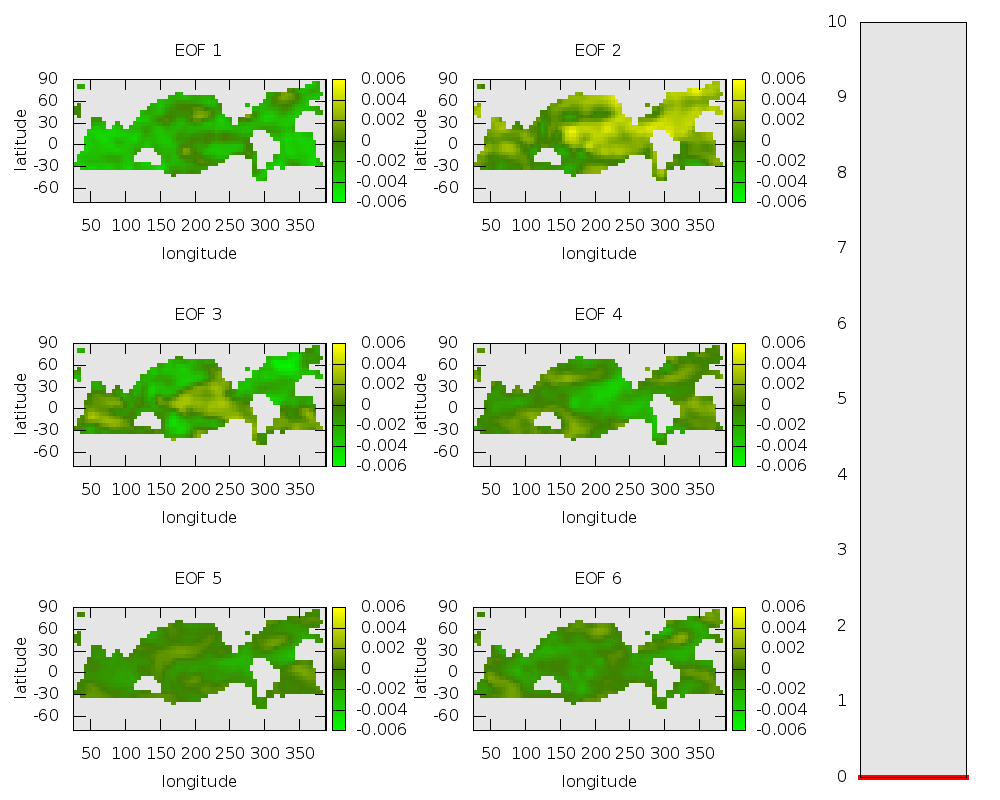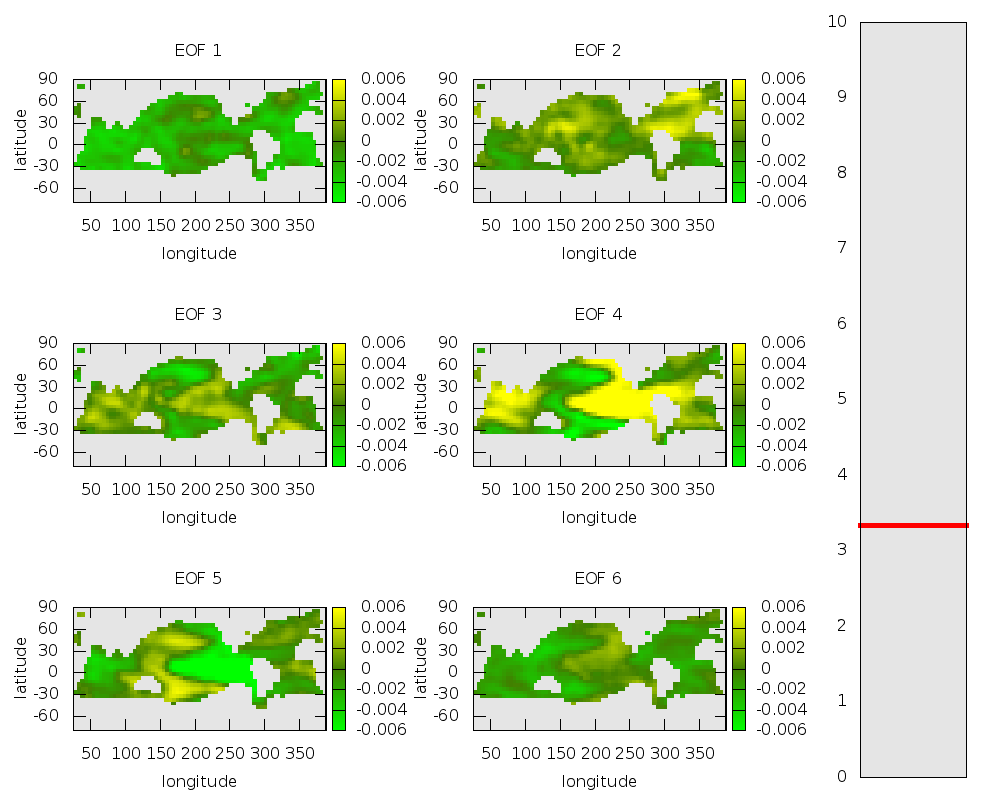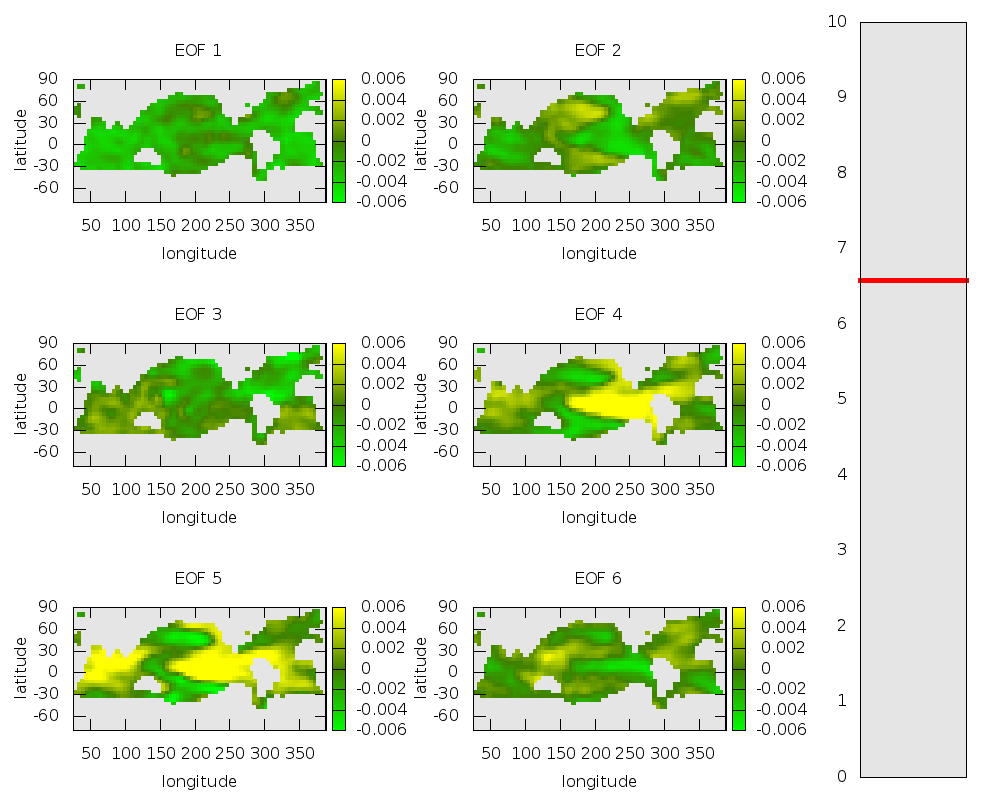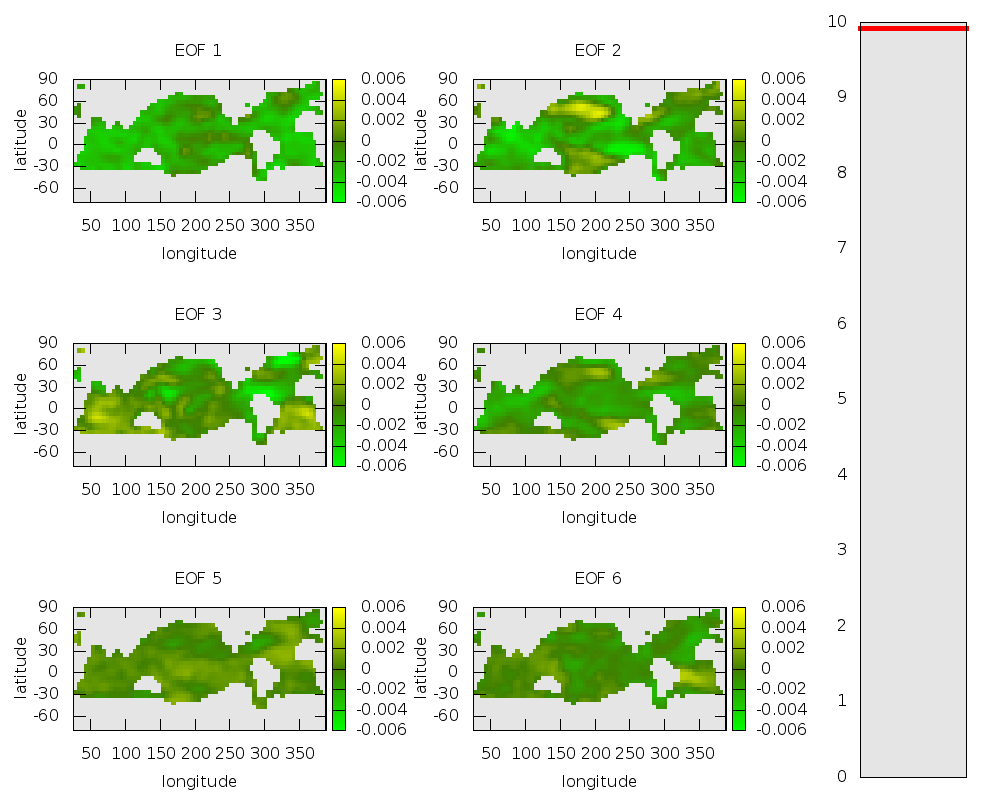
Для описания наблюдаемой высокоразмерной динамики и реконструкции ключевых свойств неизвестной динамической системы предложено использовать стохастические модели в форме случайных динамических систем. В основе такого подхода лежит гипотеза, согласно которой базовые динамические свойства системы, определяющие наблюдаемый режим поведения, могут быть описаны конечным числом степеней свободы, а остальные, не учтенные в этих уравнениях мелкомасштабные процессы имеют вид стохастического возмущения, не однородного по фазовому пространству. Важным преимуществом стохастического описания является существенно более широкий класс систем, для которых такое описание становится адекватным. Как правило, временные ряды, наблюдаемые в реальном эксперименте, короткие и/или зашумленные, что не позволяет ни оценить размерность вложения, ни установить факт детерминированности породившей их системы как таковой. В такой ситуации стохастическое описание становится существенно более адекватным, поскольку не базируется на этих оценках.
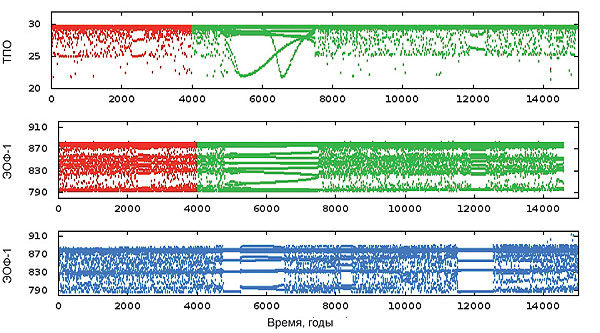
Разработанный подход был успешно применен к анализу временных рядов различной природы и построению прогноза эволюции сгенерировавших их систем. В частности, проведен анализ временных рядов, порожденных разного уровня сложности моделями атмосферно-океанической системы, лежащей в основе явления Эль-Ниньо – аномальных осцилляций температуры поверхности Тихого океана в его экваториальной части. С помощью эмпирических моделей продемонстрирована возможность корректного прогноза критических переходов – существенных качественных изменений наблюдаемой динамики системы.