Внутренние волны в океане
Другой важнейший тип волн, во многом определяющий нелинейную динамику верхнего слоя океана, – внутренние волны (ВВ), которые формируются в области наибольших градиентов верти-кально-неоднородного профиля плотности океанической воды – в области пикноклина. Основную роль в формировании пикноклина играет стратификация глубинного профиля температуры. Это важное обстоятельство было положено в основу создания масштабной лабораторной модели верхнего слоя океана, успешно реализованной под руководством В. И. Таланова в Большом термостратифицированном бассейне ИПФ РАН.
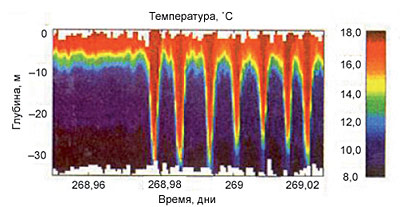
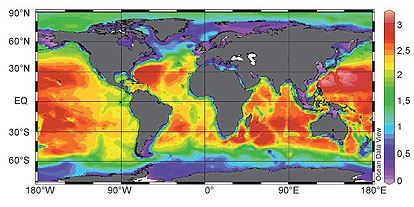
Наблюдения ВВ в океане, существующих благодаря его вертикальной плотностной стратификации, демонстрируют наличие сильно нелинейных уединенных импульсов, высота которых может достигать 50–100 м. Для их описания в ИПФ применяются различные модели: от слабонелинейных, основанных на обобщениях уравнений Кортевега – де Вриза и Гарднера, до сильно нелинейных (модели Камасса – Чоя и Островского – Гру). В рамках этих моделей изучены условия существования римановых волн, солитонов и бризеров ВВ и исследовано их взаимодействие между собой и с внешними полями. Структура солитонов определяется знаками коэффициентов квадратичной и кубической нелинейности, а бризеры возможны только при положительности коэффициента кубической нелинейности. Построены карты распределения кинематических характеристик ВВ в Мировом океане. Разработана модель трансформации ВВ в шельфовой зоне с учетом переменности гидрологии по трассе распространения, эффектов Кориолиса и диссипации, позволившая провести численное моделирование параметров ВВ на различных шельфах, в том числе в Арктическом бассейне, и выполнить сопоставление с данными наблюдений. Выяснены физические механизмы существования аномально больших короткоживущих внутренних волн (аналогов волн-убийц) – модуляционная неустойчивость, трансформация на нелинейных «каустиках», дисперсионное фокусирование – и предсказано их возможное появление в Балтийском и Южно-Китайском морях (Е. Н. Пелиновский, Т. Г. Талипова; К. А. Горшков, И. А. Соустова).
Среди работ ИПФ в области гидрофизики значительное место занимает изучение взаимодействия волн различных пространственных и временных масштабов. Взаимодействие поверхностных и внутренних волн – один из наиболее интересных примеров такого взаимодействия в природных условиях. Сотрудниками ИПФ было показано, что физические механизмы воздействия ВВ и создаваемых ими подповерхностных течений на ветровое волнение существенно различны в разных диапазонах ветровых волн. В диапазоне метровых и дециметровых волн определяющую роль играет механизм, связанный с непосредственным влиянием переменного подповерхностного течения, создаваемого ВВ, на кинематику поверхностных волн. Соответствующая ему модель изменения характеристик поля ветровых волн под действием ВВ, развитая под руководством В. И. Таланова, была названа кинематической моделью. Она получила многократные экспериментальные подтверждения в лабораторных и натурных условиях (В. В. Баханов) и широко известна среди специалистов. В высокочастотной части спектра волнения (сантиметровая и миллиметровая рябь) основную роль играют другие эффекты, в частности модуляция коэффициента затухания поверхностных волн вследствие перераспределения под действием ВВ пленок поверхностно-активных веществ (С. А. Ермаков). Имеются экспериментальные данные, указывающие на существенную роль каскадных механизмов воздействия ВВ на короткие (сантиметровые) ветровые волны: течение, создаваемое на поверхности ВВ, трансформирует метровые и дециметровые волны, а они воздействуют на сантиметровую рябь. Кроме того, неоднородное поле течений, созданное ВВ, вызывает изменчивость поля скорости ветра над водной поверхностью, что приводит к модуляции инкремента мелкомасштабных ветровых волн (Ю. И. Троицкая).
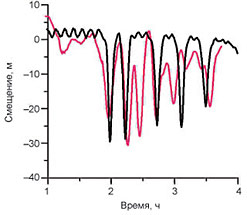
Исследование взаимодействия волн с неоднородными течениями также занимает важное место в тематике гидрофизических исследований. Особый интерес представляет нелинейное взаимодействие ВВ с потоками в окрестности так называемых резонансных уровней – критических слоев, где фазовая скорость волн совпадает со скоростью потока. Такое взаимодействие может вызвать существенную перестройку течения из-за обратного воздействия волны на течение в результате резонансного обмена импульсом. В рамках развитой Ю. И. Троицкой квазилинейной модели турбулентного следа за телом, буксируемым в стратифицированной жидкости при больших числах Рейнольдса и Фруда, показано, что основным механизмом эволюции следа является развитие гидродинамической неустойчивости возбуждаемого телом струйного течения. Численные и лабораторные эксперименты подтвердили адекватность предложенной модели, и следующие из нее результаты по эволюции поля скорости в следе (средние параметры следа) определяются из модели с точностью до единиц процентов.
В последнее время исследователей заинтересовали физические явления, происходящие при истечении пресных сточных вод из коллектора подводной сбросовой системы в стратифицированный океан. Необходимость понимания и прогнозирования этих процессов обусловлена актуальными экологическими проблемами и современным развитием аэрокосмических дистанционных методов мониторинга подводных систем сброса сточных вод. Масштабное моделирование в БТСБ показало, что формирующиеся в этом процессе всплывающие струи возбуждают интенсивные короткопериодные ВВ при взаимодействии с пикноклином. На основании анализа зависимостей амплитуд генерируемых волн от характеристик струйного течения и стратификации предложен механизм генерации волн, связанный с возбуждением автоколебаний глобально неустойчивой моды при взаимодействии всплывающей струи с пикноклином (Ю. И. Троицкая, Е. В. Ежова, В. И. Казаков, Д. А. Сергеев).
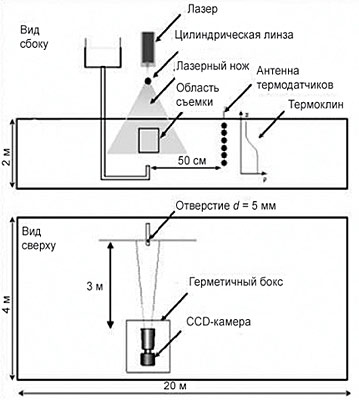
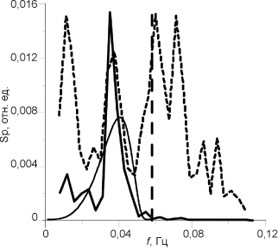
Чтобы придать комплексный характер исследованию явлений, порождаемых затопленными плавучими струями в стратифицированной жидкости, проведено прямое численное моделирование динамики фонтана, формирующегося при проникновении вертикальной струи сквозь пикноклин в стратифицированной жидкости (О. А. Дружинин). Расчеты показали, что при числах Фруда, превышающих критическое значение, возникают автоколебания фонтана, сопровождающиеся генерацией ВВ в пикноклине. Изучены возможные моды автоколебаний фонтана и соответствующие им структуры излучаемых ВВ. Из данных расчетов следует, что зависимость амплитуды колебаний верхушки фонтана от числа Фруда хорошо согласуется с предсказанием теоретической модели конкуренции взаимодействующих мод в режиме мягкого самовозбуждения.
Полученные в ИПФ фундаментальные результаты теоретических и экспериментальных исследований физических механизмов воздействия ВВ и неоднородных течений на ветровые волны были положены в основу разработки и практического использования радиофизических методов и средств дистанционной диагностики верхнего слоя океана.
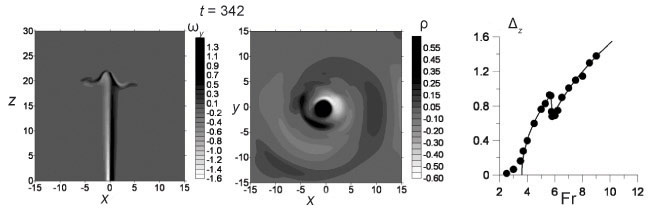
зависимость амплитуды осцилляций фонтана от числа Фруда (справа)