Микроскопическая теория критических явлений в фазовых переходах 2-го рода
Несмотря на прикладную ориентацию института, особое значение в его работе придается решению проблем фундаментальной теоретической физики. Недавно был установлен и исследован универсальный механизм фазовых переходов 2-го рода, а также сформулированы основы непертурбативной микроскопической теории критических явлений, основанной на явном выделении универсальной нелинейности (взаимодействия), которая предопределяется нарушаемой симметрией, диктуемой интегралами движения (условиями связи) в соответствии с теоремой Нетер и ответственной за фазовый переход посредством ограничения многочастичного гильбертова пространства. Показано, что этот механизм отвечает за фазовый переход в состояние с бозе-эйнштейновским конденсатом даже в идеальном газе, т. е. в отсутствие какого-либо межчастичного взаимодействия (В. В. Кочаровский, Вл. В. Кочаровский).
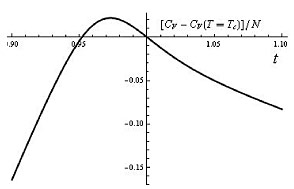
Впервые найдено и описано точной аналитической формулой универсальное вероятностное распределение числа частиц в бозе-эйнштейновском конденсате идеального газа в мезоскопической ловушке с произвольными температурой, объемом и числом частиц. Сформулированы точные соотношения самоподобия термодинамических и статистических величин для мезоскопического бозе-эйнштейновского конденсата в идеальном газе. Аналитически найдено универсальное критическое поведение теплоемкости в лямбда-точке для идеального газа с бозе-эйнштейновским конденсатом в мезоскопической ловушке. Показано, что полученные результаты для параметра порядка и всех высших моментов флуктуаций конденсата выходят на известные асимптотики по обе стороны от критической области (теория Ландау) и согласуются с частными результатами ренорм-группового анализа, справедливого в узкой центральной части критической области.